How do I get started?
It can be daunting to learn a new program, let alone teach it to your students. In this document you will find a suggested list of puzzles to assign to your students when you are just beginning. Each topic will list about a dozen puzzles you can use to introduce the CanFigureIt software to your class. Each list will start with very easy puzzles to solve and gradually get more difficult. The idea is for students to learn how to use the CanFigureIt platform as a vehicle to understand the proof process. It’s okay if you are unsure of how to solve these puzzles from time to time. Work together with your students and watch them get excited about helping the teacher. It’s the sticking points that bring out the rich conversation and teachable moments in the classroom. So have no fear. Remember that you CanFigureIt out, and in doing so provide a great example for your class. If all else fails, you can always reach out for help at support@canfigureit.com. The customer support unit is super friendly and quick to respond. Now, let’s get started!
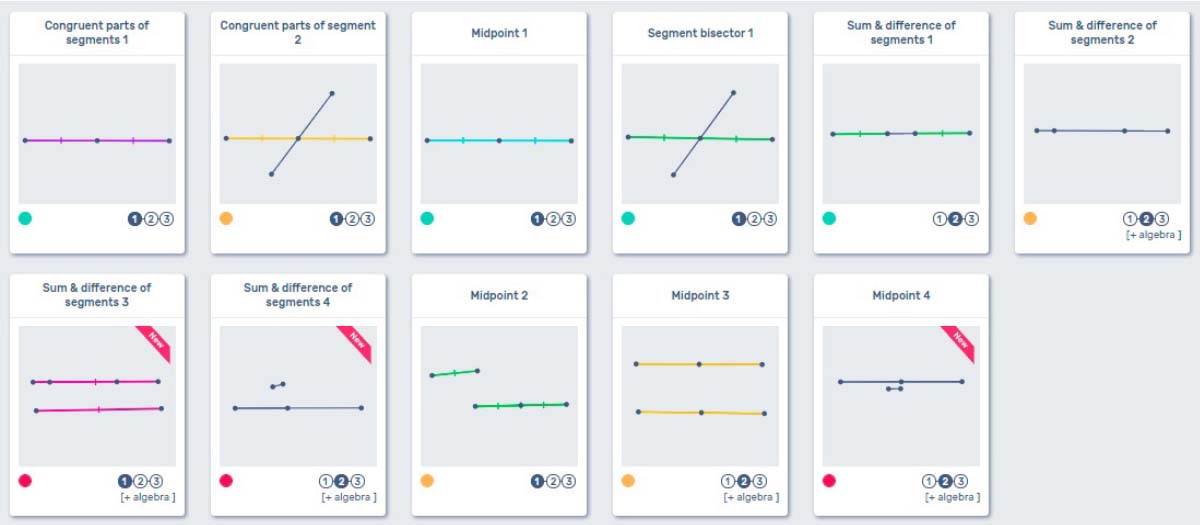
Points and Segments
A good time to start using CanFigureIt with your students is at the very beginning of the school year. Most of the puzzles you will find listed below get right to the point… Well, points and segments anyway. This section is all about segment addition, midpoints, and algebraic justification. Most students coming from Algebra I will have a foundation from their Algebra class that should allow them an entry point into this topic. It is recommended that you discuss the Segment Addition Postulate with your students prior to or after using these puzzles.
Puzzles List
- Congruent parts of segment 1
- Congruent parts of segment 2
- Midpoint 1
- Segment bisector 1
- Sum & difference of segments 1
- Sum & difference of segments 2
- Sum & difference of segments 3
- Sum & difference of segments 4
- Midpoint 2
- Midpoint 3
- Midpoint 4
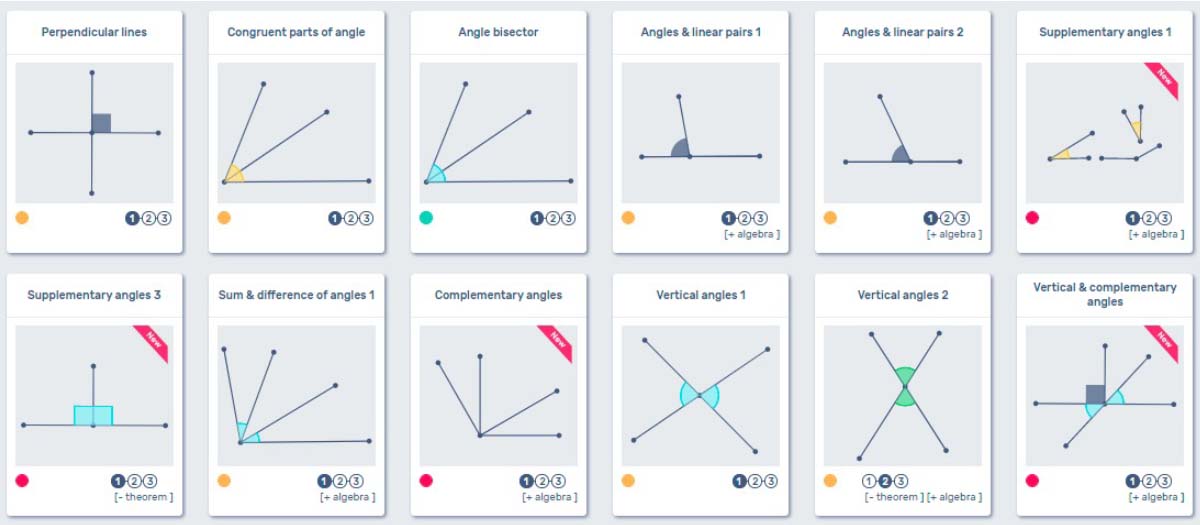
Angle Pairs
Now that you have gotten your feet wet you can move on to the angle pairs section. Here you will continue using algebra, but you will start to see some of the puzzles have this symbol [– theorem]. This means that the theorem that could be used to solve the puzzle directly will not be available. Here is a good time to establish that theorems must be proven before they can be used. Introducing terms such as complementary, supplementary, and vertical angles should also be done here.
Puzzles List
- Perpendicular lines
- Congruent parts of angle
- Angle bisector
- Angles & linear pairs 1
- Angles & linear pairs 2
- Supplementary angles 1
- Supplementary angles 3
- Sum & difference of angles 1
- Complementary angles
- Vertical angles 1
- Vertical angles 2
- Vertical & complementary angle
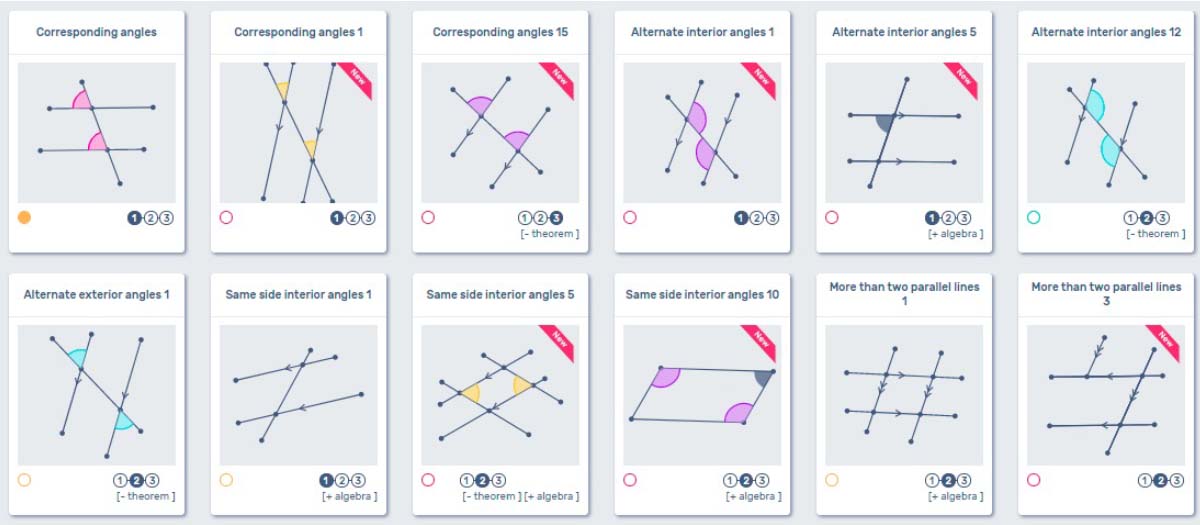
Parallel Lines
Typically, we discuss the pairs of angles formed when parallel lines are cut by a transversal all together. The following list will give you a mix of puzzles to use once you have discussed this section with your class (or after if you prefer). This section is quite robust with puzzles, so feel free to look around for others you can use. It would be a great time to use CanFigureIt to teach these angle pair relationships during class time. Have fun watching your students teach each other how to solve these puzzles. They won’t even realize they are “Doing Math”.
Puzzles List
- Corresponding angles
- Corresponding angles 1
- Corresponding angles 15
- Alternate interior angles 1
- Alternate interior angles 5
- Alternate interior angles 12
- Alternate exterior angles 1
- Same side interior angles 1
- Same side interior angles 5
- Same side interior angles 10
- More than two parallel lines 1
- More than two parallel lines 3
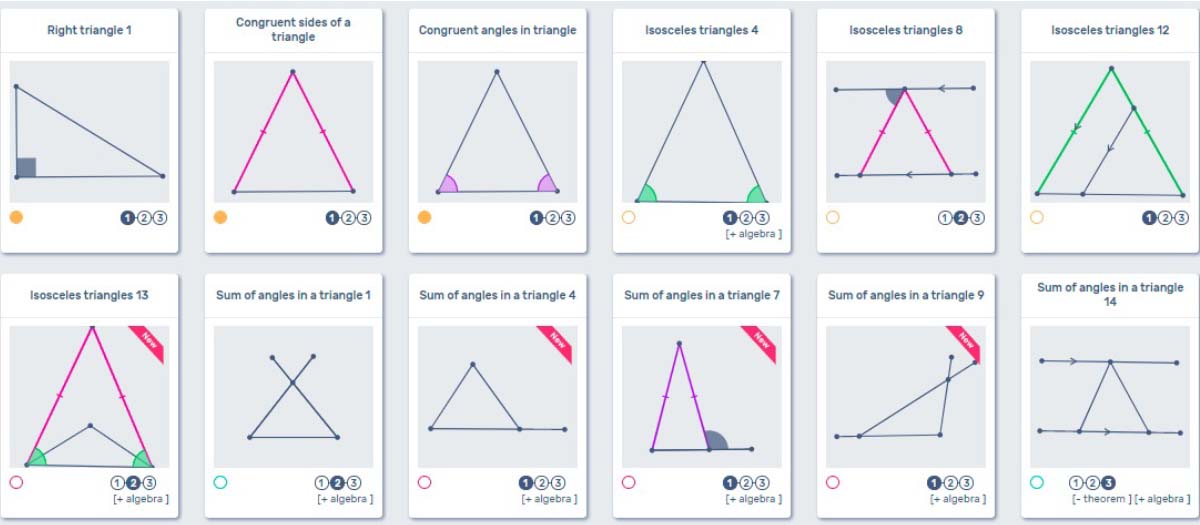
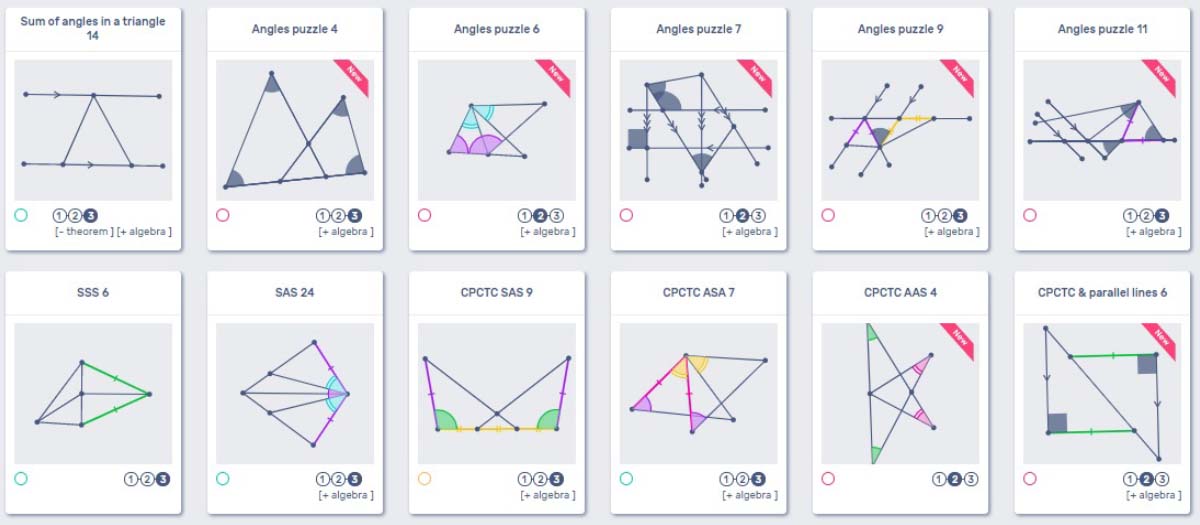
Triangle Properties
Here we are starting to build something with our students. The discussion of triangle properties here gives us a chance to connect our knowledge from previous sections with new content. Students will focus on isosceles triangles as well as the triangle sum theorem. Many of these proofs require the use of theorems or concepts gained in previous sections. Angle addition, supplementary pairs, parallel lines and many other ideas will all be necessary in this portion of the CanFigureIt software. You and your students will have graduated from learning how to use the software to using the software to understand the geometry concepts in a way that allows for true understanding.
Puzzles List
- Right triangle 1
- Congruent sides of a triangle
- Congruent angles in triangle
- Isosceles triangle 4
- Isosceles triangle 8
- Isosceles triangle 12
- Isosceles triangle 13
- Sum of angles in a triangle 1
- Sum of angles in a triangle 4
- Sum of angles in a triangle 7
- Sum of angles in a triangle 9
- Sum of angles in a triangle 14
Congruent Triangles
The list of puzzles here is twice as long as others, but there is so much that can be done on this topic in the CanFigureIt platform. Everything related to congruent triangles has multiple puzzles that can be assigned to your class. Feel free to poke around the library to pick and choose what works for you and your students. Below is a list of puzzles that will challenge your students with everything from SSS to CPCTC. Now try saying CPCTC 5 times as fast as you can. Seriously, it’s really funny to watch the kids try this!
Puzzles List
- SSS 1
- SSS 4
- SSS 7
- SAS 1
- SAS 7
- SAS 9
- SAS 16
- SAS 24
- ASA 1
- ASA 3
- ASA 5
- ASA 10
- AAS 1
- AAS 2
- HL 1
- HL 8
- CPCTC SSS 5
- CPCTC SAS 5
- CPCTC ASA 2
- CPCTC AAS 2
- CPCTC HL 5
- CPCTC & parallel lines 5
- Overlapping triangles 2
- Congruence & parallel lines 1
Similar Triangles
In this section there are only a handful of puzzles, but they are effective. The directions like the puzzles are “similar” to what we have already seen. The first 6 puzzles are relatively straight forward, while the second half of them offer a real challenge. This set offers excellent practice opportunities for students. While the names of these puzzles are a clue to their solutions, students will still be pushed here.
Puzzles List
- Similar triangles AA 1
- Similar triangles AA 2
- Similar triangles AA 3
- Similar triangles AA 4
- Similar triangles SAS 1
- Similar triangles SAS 2
- Similar triangles SAS 3
- Similar triangles SAS 4
- Similar triangles SAS 5
- Similar triangles SAS 6
- Similar triangles SSS 1
- Similar triangles SSS 2
Quadrilaterals (Parallelograms)
We are going to split up the quadrilateral section into more manageable parts here. The largest part is about parallelograms. The focus should be to define what makes a quadrilateral a parallelogram. We can do this by showing both pairs of sides parallel… You know the rest. In this set we start with puzzles that reinforce the ways this can be shown with simple proofs at first. Of course, we step it up in the second half of these problems. Again, feel free to choose different puzzles for your students. There are plenty of options here.
Puzzles List
- Sides of parallelogram 1
- Sides of parallelogram 2
- Angles of parallelogram
- Diagonals of parallelogram
- Parallel sides in a quad
- Congruent sides in a quad
- Congruent not right angles
- Properties of parallelograms 1
- Properties of parallelograms 3
- Properties of parallelograms 11
- CPCTC in a parallelogram 11
- CPCTC in a parallelogram 13
Quadrilaterals (Rectangles, Rhombi & Squares)
Now we will combine the three special parallelograms together. Some of these puzzles will require the students to establish a quadrilateral is a in fact a parallelogram prior to moving onto hitting the target. So, it would be wise not to skip the previous section. And don’t forget to use your corny math jokes here.
Puzzles List
- Properties of rectangles 1
- Congruent triangles in a rectangle 1
- Congruent triangles in a rectangle 2
- Congruent triangles in a rhombus 1
- CPCTC in a rhombus 1
- CPCTC in a rhombus 5
- Properties of squares
- Congruent triangles a in square 1
- CPCTC in a square 1
- Angles measurements in a rhombus 2
- Angles measurements in a square
- Diagonals of a rectangle
Quadrilaterals (Trapezoids & Kites)
Now we can focus our attention to the quadrilaterals that have one or zero pairs of opposite parallel sides. Just like in the other quadrilateral sections our preliminary puzzles are simple to solve by knowing the theorems for their respective shapes. The rest of the puzzles require students to combine the skills and theorems from earlier sections to reach the target. If your students have been using the software from the beginning, there is no doubt that they will be able to teach you how to solve these proofs. Keep up the good work, the students are well on their way to Proof Ninja status.
Puzzles List
- Opposite sides of trapezoid
- Angles of isosceles trapezoids
- Sides of a kite 1
- Diagonals of a kite
- Properties of trapezoids 1
- CPCTC in a trapezoid 2
- CPCTC in a trapezoid 6
- Congruent triangles in a kite 1
- Congruent triangles in a kite 3
- CPCTC in a kite 3
- Angles measurements in
a trapezoid 1 - Angles measurements in
a trapezoid 2
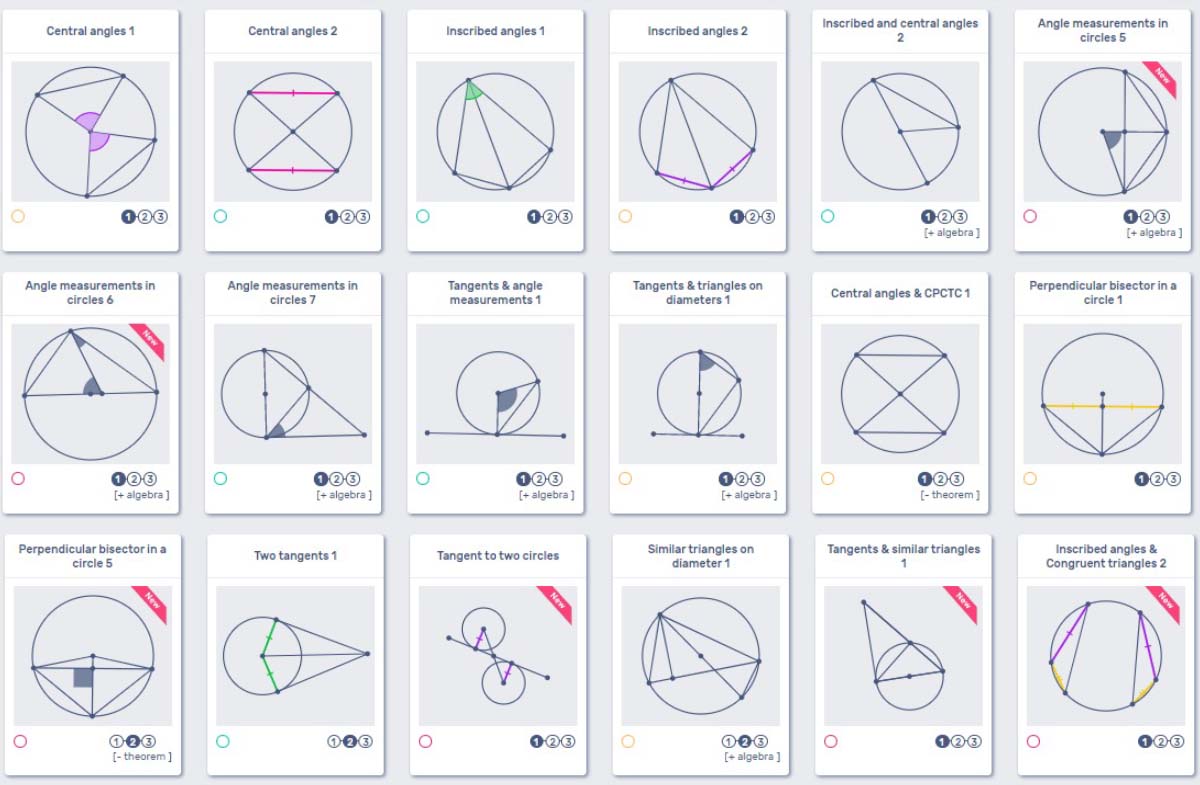
Circles
So, we have reached the last section. Typically, the circle section in most curriculum takes quite a while to complete. There are many puzzles listed below, so again use your best judgement when getting “a-round” to these with your class. However, your students are ready.
They CanFigureIt…
Puzzles List
- Central angles 1
- Central angles 2
- Inscribed angles 1
- Inscribed angles 2
- Inscribed and central angles 2
- Angle measurements in circles 5
- Angle measurements in circles 6
- Angle measurements in circles 7
- Tangents & angle measurements 1
- Tangents & triangles on diameters 1
- Central angles & CPCTC 1
- Perpendicular bisector in a circle 1
- Perpendicular bisector in a circle 5
- Two tangents 1
- Tangent to two circles
- Similar triangles on diameter 1
- Tangents & similar triangles 1
- Inscribed angles &
Congruent triangles 2
Bonus Section - Challenge Puzzles
Congratulations if you made it this far. Below is a list of some really challenging problems. If you can finish these then you are officially in the Dojo with the rest of the Proof Ninjas.
Welcome, I knew you could do it!
Puzzles List
- Sum of angles in a triangle 14
- Angles puzzle 4
- Angles puzzle 6
- Angles puzzle 7
- Angles puzzle 9
- Angles puzzle 11
- SSS 6
- SAS 24
- CPCTC SAS 9
- CPCTC ASA 7
- CPCTC AAS 4
- CPCTC & parallel lines 6
